[7차] Recommender Systems - Rating

추천 시스템의 평점 예측 방법인 유사도 기반 협업 필터링과 행렬 분해 기법에 대해 설명합니다. 코사인 유사도를 활용한 아이템 기반 협업 필터링의 계산 과정과 메모리/계산량 문제를 해결하는 행렬 분해 방식의 경사하강법 구현, 과적합 방지를 위한 정규화 기법을 다루고 있습니다.


Recommender System : 사용자 (user) 개인의 취향에 맞춘 온라인 상의 아이템(Item, 상품 등)을 추천하는 시스템

  • 추천 시스템의 방법중에서 “Rating Prediction(=평점 예측)” 방식을 공부해보려고 한다.

  • 대표적 알고리즘 2개인 Similarity Based Collaborative Filtering 과 Matrix Factorization 에 대해서 알아보겠다.



Similarity Based Collaborative Filtering

한국어로 유사도 기반 협업 필터 라고 한다.

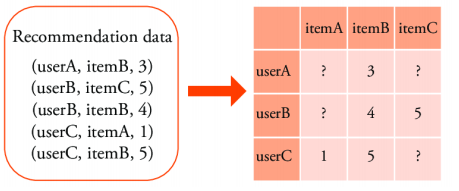
즉, 아래 행렬의 ? 를 예측하는 것이다.

  • 행 : 사용자(user)
  • 열 : 아이템(item)
  • 요소 : 점수(rating)

image-20230604145721184



공식

아이템 기반 협업 필터 (Item-based CF) 식을 소개한다.

  • i : 예측하려는 item
  • i’ : 실제 추천 후보 item
  • 아래 식의 핵심은 유사도 * 실제 평점 과 Normalization 이다.

image-20230604145934080


Normalization은 말그대로 정규화 때문에 사용하는 것이며, 여기선 0~1로 정규화를 하는게 아니라 실제score(점수)가 0~5이기 때문에 0~5범위로 만들어준다.

유사도(sim)는 정확히 말하자면 코사인 유사도 이다. 따라서 코사인 유사도 공식 을 사용한다.

  • Cosine Similarity(코사인 유사도) 는 각도의 유사도를 측정하는 동작을 한다. 그래서 벡터(크기, 방향)를 사용한다.


아래부터는 user1의 Titanic 의 평점을 예측하는 과정을 나타내보겠다.

1. 예측에 필요한 sim 들을 구한다.

  • 이때, user1은 Batman, Ironman만 실제 평점(=r)을 가지기 때문에 해당 2개의 영화랑만 유사도를 측정
    • WHY?? -> Spiderman처럼 값이 없는 경우 r=0이기 때문(r은 실제 user1의 Spiderman 평점)
  • 또한, 두 영화(=i)가 겹치는게 없다면 유사도(sim)이 0이 나온다.
    • 실제로 sim(ironman, titanic) 을 보면 0이 나옴을 알 수 있다.

image-20230613215502177


2. 구한 값들을 이용해서 suser1,Titanic 을 구한다.

  • user1의 Titanic 의 예측 점수가 4 점이라는 결론을 내릴 수 있다.

image-20230604151114601



Matrix Factorization

한국어로 행렬 분해 라고 한다.

Objective Function(=목적, 오차, 손실, 비용함수) 을 최소화 하는 P, Q 값을 계산.
물론 P, Q 값의 초기값은 임의로 설정후 P, Q 값을 update 해나가는 것이다.

앞서 소개한 유사도 기반 협업 필터 의 단점 때문에 행렬 분해 를 사용하게 되었는데, 비교해보자.

  • 유사도 기반 단점
    • 계산을 위해 Rating Matrix를 모두 메모리에 올려야 한다. (높은 메모리 요구량)
    • 하나의 Item 예측에 여러 Item들 유사도를 계산해야 한다. (높은 계산량)
    • 두 아이템을 공통적으로 소비한 사용자가 적어도 한 명 필요하다. (한계)
  • 행렬 분해 장점
    • 분해한 P, Q 행렬의 크기는, Rating Matrix보다 매우 작다. (낮은 메모리 요구량)
    • 두 벡터의 내적만 계산한다. (낮은 계산량)
    • 두 아이템을 공통적으로 소비한 사용자가 없어도 계산 가능하다.

공식

이 행렬 분해의 핵심은 아래 수도 코드가 전부이다.

  • 참고 링크 : 경사하강법
    • 우린 W가 아닌 P, Q를 Update 하게 된다.

image-20230604154827038


Objective Function 의 공식

image-20230604154400310


위의 Objectiv Function을 최소화 시켜야 하므로 이때 Stochastic Gradient Descent 사용

아래는 공식을 풀어낸 모습을 나타낸다.

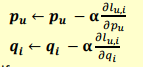
image-20230604154555539

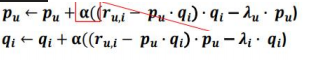
=> image-20230604154616412


아래 식의 의미는 수많은 iterate(순회)에도 이전 오차와 현재 오차의 크기 가 큰 변화가 없을 시 설정한 iterate 반복 횟수를 채우기 전에 유도리 있게 break를 한다는 것이다.

image-20230604155157694


추가로 여기서 사용한 Regularization(규제)를 좀 더 설명해보겠다.

아래 빨간글자가 “규제” 부분인데 이 값이 당연히 클수록 “l(목적함수) 값”은 커지니까 오차가 크다고 해석할 수 있으며, “학습”의 목적은 이 오차를 줄이는것이기 때문에 이에따라 “가중치”가 줄어들게 된다.

image-20230613220427967


해당 “규제”를 하는 이유는 아래의 내용처럼 Overfitting(과적합)을 방지하기 위해서이다.

image-20230613220751259

image-20230613220834073



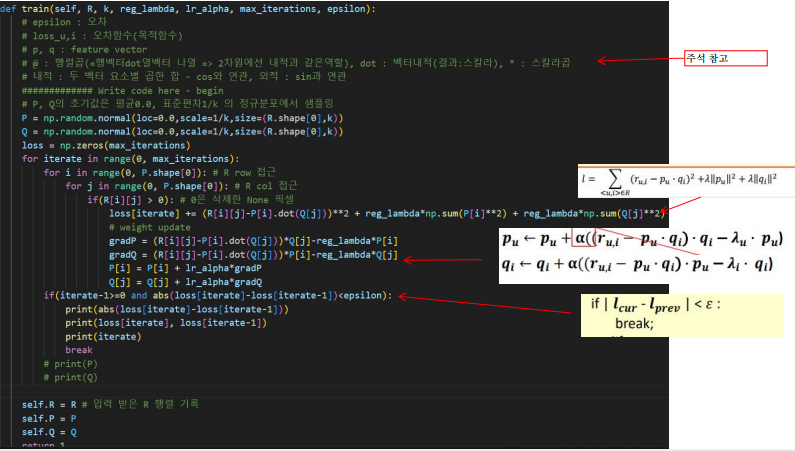
구현 예시

실제 구현했을때 코드의 예시

  • 자세한것은 아래 링크 참고

image-20230613221025063

댓글남기기

참고