미분(적분) 기본
복소평면, 허수, 파이, 자연상수의 개념부터 미분의 기본 원리, 다양한 미분 공식(삼각함수, 로그함수, 지수함수), 편미분, Chain Rule까지 설명하고, 적분의 기본 개념과 부정적분/정적분 공식들을 포함하고 있습니다.
수학을 정말 자세히 설명할 생각은 없다.
그저 머신러닝(딥러닝) 공부에 도움이 될 기초 수학 지식들을 정리할 생각이다.
미분(적분) -> 확률 순서로 정리하겠다. (사진이 너무 악필이네ㅠㅠ)
미분(기초수학 ver) => 기울기
1. 복소평면(직교좌표/극좌표)
허수(i)
잘 생각해보면 우리는 x^2은 양수라고 본능적으로 생각하고 있다.
그런데, x^2 은 음수는 아닌가?? 그걸 알 수 있나?? 이런 이유 때문에 “허수” 라는 개념이 탄생한다.

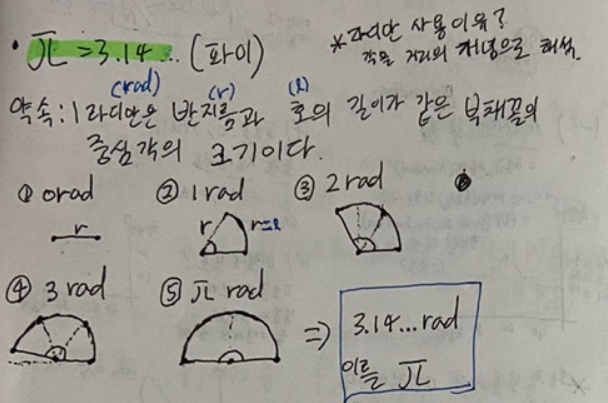
파이(π=3.14)
우리는 라디안이라는 개념을 사용하는데, 이는 각도를 거리의 개념으로 해석하기 위해서 사용한다.
그렇다면 90도 일때는 몇 라디안 일까?? 라는 의문을 해결하기위해 탄생한게 파이(=π)이다.
90도는 3.14xxx 라디안이라고 정의한 것이다.
+) 자연상수(e=2.7xxx)
고등학교때 미분에서 많이보던 공식이 lim(1+1/n)^n 관련 식이였다.
해당 식에서 n의 숫자를 키우면 2, 2.25, ... , 2.7xxx 이하 가 나오는 신기한 특징이 있다.
n을 제일 큰 무한대로 보냈을 때의 값을 정의하기 위해 자연상수 e가 탄생한다.
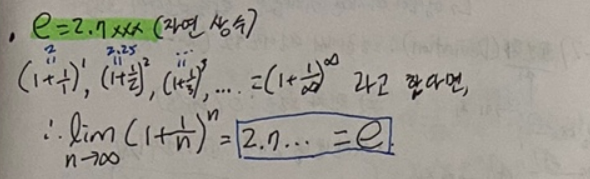
복소평면(직교좌표/극좌표)
삼각함수를 활용해서 복소평면의 예를 보여주겠다.
%20%EA%B8%B0%EB%B3%B8/image-20230419172251461.png)
2. 미분 개념
%20%EA%B8%B0%EB%B3%B8/1-16818932251771.png)
3. 미분 공식들
미분법의 기본 공식
문제를 풀때 x를 f(x)로 생각해서 문제를 푸는게 좋다.
%20%EA%B8%B0%EB%B3%B8/image-20230419173953111.png)
삼각함수 미분 공식
%20%EA%B8%B0%EB%B3%B8/image-20230419174635461.png)
로그함수와 지수함수 미분 공식
%20%EA%B8%B0%EB%B3%B8/image-20230419174746809.png)
4. 편미분
이때까지 변수가 x 한개 일때만을 봤다면, 이제는 변수가 2개 이상일때를 본다.
- x로 미분했을때, y로 미분했을때의 결과를 각각 보여준다.
%20%EA%B8%B0%EB%B3%B8/image-20230419174916931.png)
5. Chain Rule
우리가 기본으로 기억하는 y=f(x) 의 경우 x변화에 따른 y변화량을 바로 알 수 있다.
그런데 아래 그림처럼 중첩 함수로 이루어진 경우 x변화에 따른 i변화량을 바로 알기 힘들다.
이때, Chain Rule 을 사용해서 구한다.
%20%EA%B8%B0%EB%B3%B8/image-20230419175008264.png)
적분(기초수학 ver) => 면적
부정적분은 구간을 정하지 않으므로, 적분 상수가 따로 존재
정적분은 구간을 a, b 로 있으므로 적분 상수가 존재하지 않음
적분 공식들
부정적분 기본 공식
%20%EA%B8%B0%EB%B3%B8/image-20230419175642651.png)
정적분 기본 공식
%20%EA%B8%B0%EB%B3%B8/image-20230419180010469.png)
삼각함수의 적분 공식
%20%EA%B8%B0%EB%B3%B8/image-20230419175915621.png)
지수함수와 로그함수의 적분 공식
%20%EA%B8%B0%EB%B3%B8/image-20230419180223002.png)
부분적분 공식
%20%EA%B8%B0%EB%B3%B8/image-20230419180318468.png)
댓글남기기