확률(선형대수) 기본

평균, 분산, 표준편차의 개념부터 가우시안 분포, 테일러 급수, 확률변수, 공분산, 상관계수, 조건부/결합/주변 확률, 베이즈 이론까지 확률 개념과 벡터, 행렬, 벡터 공간, 기저벡터, 노름, 행렬의 종류 등 선형대수 핵심 개념을 포함하고 있습니다.

확률

1. 평균, 분산, 표준편차

평균(mean)

엄밀히 따지면 “기대값” 은 일반 변수의 평균이 아닌 확률 변수의 평균이다.

현재 아래 식은 그냥 일반 변수를 사용한것이기 때문에 “기대값”은 적절한 표기는 아닌것 같긴하다.

1-2. 편차(Deviation)

편차의 평균은 항상 0이다. 그림의 왼쪽을 확인해보자.

• 이를 해결하기 위해서 편차에 절대값을 씌우거나 편차에 제곱을 하는 형태로 편차의 평균을 구할 수 있다.

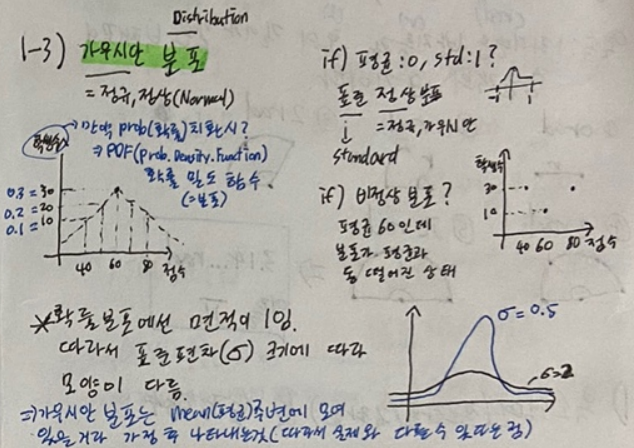
1-3. 가우시안 분포

용어 : 가우시안 분포 = 정규,정상(Normal) 분포(Distribution)

가우시안 분포는 mean(평균) 주변에 값들이 모여있을거라 가정후 나타내는 것이다.

• y축 값을 확률로 치환시 기존 분포를 PDF로 볼 수 있고, 확률분포에선 총 면적은 1이다.
• “표준 가우시안 분포” 는 “표준”이 들어갔으므로 다른 특징을 가진다.
  • 특징 : 평균 = 0, 표준편차(=std) = 1

1-4. Taylor Series(테일러 급수)

아래 그림의 우상단 그래프처럼 “복잡한 함수”를 “t=a” 라는 어떤 특정 점에서 단순한 함수로 근사화할 수 있다.

아래 예시는 sin함수를 단순화(근사화) 한 것이다.

• t=0 때를 기준으로 근사화를 한것이고, 1차식과 3차식으로 근사화한 결과를 보여준다.
• 물론, 3차식이 좀 더 정교하다.

분산(Variance)

편차 제곱의 평균이 바로 “분산”이다.

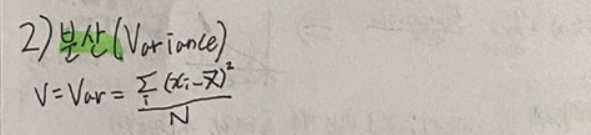
표준 편차(Standard Deviation)

분산에 루트를 씌운것이 “표준 편차”이다.

2. 확률변수(Random Variable)

앞에서 “평균” 부분에서는 일반 변수를 다뤘다면 이제부턴 확률변수를 다루는 모습을 보이겠다.

조금씩 공식들도 다르기 때문에 “일반, 확률” 변수의 차이를 잘 이해하자.

• scalar Vs. Random Variable 때 E(x), V(X) 공식 차이

3. 공분산(Covariance)

확률 변수가 2개때 “관계”

• 독립이면 COV(X,Y) = 0 이다. (관계가 없다는 의미로 0)

• COV는 값의 크기에 따른 영향을 받는다는 문제점이 있다.
  • 예) 위 그림에서 2번을 상관관계 “대”로 가정했는데, 실제론 1번이 상관관계가 더 클수도 있다

COV 문제점 해결방안

크기 문제의 해결방안으로 정규화 를 하고, 상관계수 로 비교한다.

4. 기대값(평균), 분산 특징

기대값 특징

분산 특징

5. (중요)조건부, 결합, 주변 확률 정의 + 예제

이때까지 수학개념들은 전부 중요하긴 하지만, 특히 더 중요한 확률 정의들이니까 잘 이해해두자.

아래 그림에서 파란색 타원으로 주변확률을 나타낸 부분을 좀 더 설명하겠다.

• P(X) = ... 로 식을 나타냈는데, 정확히는 P(X=1) = ... 로 X=1 때의 확률처럼 이해해야한다.
• 즉, P(X=1) 구할때는 표에서 X=1때 세로로 값들 나열된것 전부 더하면 된다.

예제

6. (중요)Bayes 이론 정의 + 예제

정말 중요한 이론이므로 꼭 잘 기억

예제

문제

풀이

선형대수

0. 벡터, 행렬

Vecotr Space, Rank

Unit Vector

유닛 벡터란 벡터의 크기가 1인 벡터

• “야, 여”는 2개의 기저벡터(basis vector)의 조합으로 만들어진 벡터이다.

Basis Vector(Vector Space)

Basis Vector란 “기저벡터”라고 하며 “선형 독립 벡터”라고도 한다.

“선형 독립 벡터”(Linear Independent) 를 만족하면 어떠한 값도 만들 수 있다.

• 이때, WX에서 W를 “Span”이라고 함.

직교(orthogonal), orthonormal(직교+Unit)

Norm(노름. 벡터의 크기(길이)) : L1, L2

크기(길이)는 스칼라로 출력된다.

유클리안, 맨하탄 방식 많이 사용

Matrix 종류

벡터의 부호